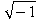O miejscu liczby traktatu zarysKto z woli i myśli zapragnie1
Kiedy słyszę, że matematyka jest królową nauk, przypomina mi się scena z filmu Brooksa: „Pan X.!Ach, to ten aktor sławny w Warszawie na cały świat...”2
Przykładowo, stosunki między matematyką a fizyką odpowiadają bardziej układowi z książki Twaina3, przy czym matematyka jawi się nieśmiało owym księciem tytularnym, którego żebrak w łaskawości swej poucza, gdzie na dworze empirii skierować swe ruchy, aby nie popełnić gafy...
Czy ta odległość istnieje, Mr Johns?
Kto przy zdrowych zmysłach powątpiewa w istnienie odległości między niniejszym tekstem (kartką papieru) a czytającym go okiem? Raczej nikt. A jej istnienie matematyczne, w postaci liczby wyrażającej wynik pomiaru, zależy od wzorca jednostki długości oraz używanej algebry liczb. Jeżeli wzorcem długości jest metr4, a liczbami znanymi badaczowi - tylko liczby naturalne5, wówczas odległość oka od niniejszego tekstu nie zaistnieje. Odległości, jakie możemy zapisać, są bowiem następującym zbiorem: jeden wzorzec metra, dwa wzorce metra, trzy wzorce metra, itp. Wszelako rzadko kto czyta "Fantastykę", trzymając ją w takim oddaleniu6 A istnienie innych liczb niż naturalne wcale nie było zawsze tak oczywiste jak dzisiaj, czego przykładem – przygoda z trójkątami pitagorejskimi.
Koszula bliższa ciału - dlaczego wolimy liczby całkowite.
Ten sposób liczenia7 niesie w sobie jakiś ładunek antropocentryzmu, a przy tym dużo ciepła pierwotnego związku człowieka z przyrodą ożywioną. Liczba sąsiadów, albo współplemieńców w gromadzie nie może być liczbą niecałkowitą, ani ujemną. Sąsiad, człowiek, albo jest, albo go nie ma. Jeżeli krokodyl odgryzie komuś nogę, albo rozeźlony gracz w kości utnie komuś ucho, to ofiara dalej jest jednym człowiekiem, a nie 0,83 ani 0,97 człowieka. Podobnie świnka czy kurka w zagrodzie: albą są, albo ich nie ma. Dwie pełne tuszki wieprzowe nie dają jednej świni. Tak samo "podział" danego człowieka na bardziej drastyczne fragmenty powoduje, że nie zalicza się już go w poczet krewnych ni znajomych. Przejrzysty, czytelny i wygodny świat dyskretnego zbioru liczb całkowitych. A każda z nich, jak samotny atom Fenicjan8, odległa od sąsiadów o tę samą niepodzielność - to robi wrażenie. Musiało wywrzeć piętno na rachunkowych przyzwyczajeniach ciekawskich starożytnych.
Liczby należą do świata idei, wykresy i rysunki zaś - dobitnie do świata empirii. Że matematyka nie zawsze umiała dogadać się z rzeczywistością dowodzą dzieje trójkąta, który urzekł starożytnych magią liczb.
Matematyka liczb kontra fizyka geometrii.
Przedmiotem sporu owych dwóch światów były pochodne "trójkąta egipskiego"9, którego długości boków mają się do siebie jak 3:4:5. Pitagorasowi przypisujemy spostrzeżenie, że 32 + 42 = 52. On niebłahe to stwierdzenie uwolnił od konkretnej postaci liczbowej nadając postać czystej idei: a2 + b2 = c2.
Jeżeli do ciekawych przymiotów trójkąta egipskiego dodać pole jego powierzchni - liczba 6, to otrzymujemy nowy związek liczbowy: 32 + 42 + 52 = 62! Obwód tego trójkąta wiąże ze sobą z kolei dwie pierwsze liczby tego szeregu i wynosi 12. Wynik ten można również uważać za rozszerzenie grona pojawiających się liczb o liczbę 2, a to ponieważ 12 = 2 * 6 (i jak tu nie zgodzić się z Plutarchem, że figura ta to najpiękniejszy z trójkątów!).
Założenie, że równanie kwadratów jest konieczne i wystarczające dla powstania trójkąta prostokątnego, skłoniło myśliciela do poszukiwań pozostałych liczb (całkowitych - innych nie znał!) dających trójkąt prostokątny, nie - egipski. Pitagorejskie wzory rekurencyjne na "pozostałe" a, b, c spełniające warunek kwadratów są następujące: a = 2n + 1}, b = 2n(n + 1)}, c = 2n2 + 2n + 1, gdzie n = 1, 2, 3... Szczególny ów trójkąt egipski. Z jednej strony tak praktyczny-pomocny w przyziemnym fachu królewskich mierniczych faraona, w codzienności odzyskania miary pól zalanych przez Nil. Z drugiej strony zarzewie powyższych związków liczbowo-figuralnych. One to, magiczne związki najpierwsze, rozbudziły nadzieję na prawdziwość tezy, że podstawę ładu wszechrzeczy stanowią liczby (naturalne), ale potem bez znieczulenia, nadzieję tę z kretesem pogrzebały dowodząc rozziewu między światem wymyślonych już liczb naturalnych a rzeczywistością. Sądząc bowiem, że boki każdego trójkąta prostokątnego wyrazić można by jakimiś liczbami naturalnymi a,b,c, natrafiono na przedziwne równanie trójkąta prostokątnego równoramiennego: a2 + a2 = c2, czyli 2a2 = c2. Naturalnie, trójkąt fizycznie istnieje, natomiast warunku10 tego nijak podzielać nie chciały wyniesione na ołtarz boskości znane podówczas jedynie liczby naturalne.
Dla idealistów oczadzonych kosmogonią liczby, usiłujących zamknąć fizykę trójkąta w świecie liczby całkowitej, niepowodzenie to musiało być wstrząsem. Ale dla badacza wolnego od fanatyzmu stanowić mogło wskazówkę, iż liczby, jakie byliśmy sobie dotychczas w stanie wyobrazić, stanowią zbiór niepełny, wymagający uzupełnienia o wartości "niehumanitarne".
Na początku była harmonia.
Jednak nawet patrząc z perspektywy rozwoju nauki, zwłaszcza fizyki, trudno starożytnym zarzucać zdziwaczenie, wyłącznie fanatyzm, lub całkowite oderwanie od rzeczywistości. Wyobrażenia o harmonii liczb nie wyssali sobie przecież z palca, raczej w dzieło poszukiwań liczbowych (i geometrycznych) przelali swoje doświadczenia i wiedzę o harmonii dźwięków. A te nieuchronnie kierowały się w stronę związków liczbowych.
Czym jest harmonia? Na pierwszy rzut ucha tylko wrażeniem: artysta wie, a słuchacz czuje, że "wszystko gra", dźwięki pasują do siebie, że muzyka jest po prostu ładna.
Arytmetyka harmonii.
Najpospolitszym instrumentem muzycznym może być napięta struna11 wykonana np. z kiszki jagnięcia, które odpowiednio wcześniej podano do stołu. Trącona struna wydaje dany dźwięk. Przyciskając strunę w środku jej długości, otrzymujemy dwie struny. Każda z nich trącona daje dźwięk wyższy niż struna o poprzedniej długości. Można zestawić instrument dwustrunowy, z czego jedna jest dwukrotnie dłuższa od drugiej. Teraz nic nie stoi na przeszkodzie, aby trącić jednocześnie dwie struny, zagrać pierwszy w historii akord i przysłuchać się jego brzemieniu. Nic na przeszkodzie - poza jakże ważką uwagą, że pojawiły się liczby, mianowicie 1 oraz 2, jednoznacznie przypisane dźwiękom tego instrumentu. Teraz liczbami można wyrazić brzmienie dwutonowej melodyki! Ale przecież instrument może być bardziej rozbudowany: kilka strun, kilkanaście, kilkadziesiąt ("pra-harfy"). Może również posiadać "tylko" kilka strun (np. 6 - jak gitara) umocowanych na desce, ale za to, w poprzek której wbito progi (tak jak na gryfie gitary) lekko wystające ponad jej lico12. Teraz możliwości jest prawie bezlik13. Ileż liczb! No i magia proporcji całkowitych - teraz jakby w liczbach zawierała się cała muzyka instrumentu. Lecz magia liczb w przypadku odczuwania muzyki idzie dalej. No bo jak bardzo, na ile całkowitych części da się podzielić strunę, aby zwykły śmiertelnik odróżniał jeszcze poszczególne dźwięki wydawane przez strunę dociśniętą do kolejnego progu? Albo: tony jakich długości struny brzmią razem harmonijnie dając konsonans, a jakich – nie harmonijnie, dając dysonans14?
Najprostszą proporcją, interwałem jest 2:1 (zwane oktawą15). Następne, w sensie ułamkowym, interwały pozostające w ramach jednej oktawy to kolejno: 3:2 - kwinta, 4:3 - kwarta, 5:3 – wielka seksta, 5:4 - wielka tercja, 6:5 - mała tercja. Za dobry konsonans uważany jest jeszcze interwał: 8:5 – mała seksta. Za nieznaczne dysonanse natomiast uważa się 8:5; 9:8; 10:9; 15:8; 16:15.
Dla danego tonu, obranego za podstawowy, istnieje zatem zbiór interwałów (tworzony "w górę" i "w dół") zwany gamą danego tonu. Jedną oktawę gamy danego tonu da się, w sposób znośny dla muzyka, okroić o niektóre interwały - daje to dwie tonacje: dur, moll16, nazywane skalą harmoniczną naturalną - w przypadku tonu c daje to odpowiednio: c-moll, lub C-dur17.
Wytrawny muzyk, pisząc utwór na dany skład, wie, wyczuwa lub pamięta, w jakiej tonacji, jaka aranżacja (harmonizacja) wywoła konsonanse, a w jakiej natomiast dojdzie do dysonansu - tonacja to układ odniesienia (+ wzorzec odległości) dla piszącego i śpiewającego muzykę.
Nie, żebym się chwalił: w roku 1986 pewnego ciepłego wieczora (właściwie nocą) blisko jednego z teatros pod Akropolem, trochę nielegalnie, bo bez biletu, podsłuchałem chóru. Choć nie wiem, czy był to chór na wzór antyczny, do dziś w uszach mając jego brzmienie - potężne, lube, czyste i przejmujące - skłonny jestem uwierzyć, że harmonia konsonansów jest nieziemskiej natury. Nie mogę się przeto dziwić, że odkrywca - kronikarz "boskich interwałów" konsonansu, uczeń Pitagorasa - Archytas18, wietrząc w doznaniach harmonii iskrę bożą, oczarowany niebiańskim pochodzeniem liczb, uznał je za idee, których odbiciem jest przyroda. Rozumiem też więc, dlaczego pitagorejczycy tak oddanie poszukiwali liczbowego fundamentu wszechrzeczy, aczkolwiek nie mogę przemilczeć, ani pochwalać ich fanatyzmu, o jakim pisze Arystoteles: "Zebrali tedy i wykazywali wszelkie możliwe i niemożliwe podobieństwa pomiędzy liczbami a stanami i częściami wszechświata i całą jego organizacją. A kiedy nie szło, naciągali rzeczy gwałtem, aby się tylko nauka razem trzymała. Powiadam Wam na przykład tak: dziesiątka się im wydawała czymś doskonałym i uważali, że w niej się bez reszty wyraża i mieści cała natura liczby - zaczem powiedzieli, że ciał błądzących po niebie będzie dziesięć, a że widać takich w ogóle tylko dziewięć, wymyślili dziesiątą niewidzialną: przeciwziemię."19. Matematyka tak pojmowana musiała - prędzej, czy później - rozminąć się z rzeczami świata widzialnego.
Głos z przyszłości - harmonia jest względna.
Przykra niespodzianka czeka za to twórcę najdoskonalszego nawet instrumentu strojonego czysto20 w danej tonacji skali harmonicznej naturalnej. Jeżeli zechcemy zmodulować dany utwór, tzn. rozpocząć wykonywanie jego pierwszego dźwięku od innego miejsca (klawisza, progu, struny instrumentu nie smyczkowego) automatycznie przenosząc nutki, zaczniemy fałszować! Harmonia nie jest bowiem zjawiskiem absolutnym, lecz występuje jedynie wewnątrz danej tonacji. Jeśli przykładowo chcemy zbudować skalę G-dur rozpoczętą na kwincie g w odniesieniu do tonacji C-dur, to mamy już, co prawda, wielką tercję h, oraz (wszystkie razkreślne): kwartę 1c, kwintę 1d, sekstę 1e, bo zawierają się, w wymaganej formie, w przedłużonej skali C-dur. Natomiast w istniejącym stroju zabraknie nam21 wielkiej septymy 1fis do g, zaś sekunda dog będzie wyższa od g o tzw. komat Pitagorasa} równy 81/80!
Mówiąc najbardziej, jak się da, po ludzku: dźwięki gamy pierwotnej G budowanej na danym tonie rozminą się bardzo szybko z dźwiękami gamy wtórnej 1G budowanej na dowolnym dźwięku z gamy G. Muzyk grający na instrumencie strojonym w jednej tonacji, nie będzie w stanie akompaniować soliście grającemu na instrumencie strojonym "trochę" inaczej, od innego tonu - wykonanie zacznie zgrzytać! A potrzeby składów i wykonań są przeróżne...
Nieżyciowe i monstrualne byłoby pianino zawierające wszystkie dźwięki czystego stroju! Kłopoty ze skalą muzyczną, z brakiem absolutnego układu odniesienia - gamy w naturalnie wyróżnionej tonacji - powoduje, że dzisiaj nasze zmysły wystawione są na nieustanny fałsz i nieczystość brzemienia: w stosowanym powszechnie strojeniu równomiernie utemperowanym22 gamy chromatycznej23 oktawę podzielono na dwanaście równych przedziałów, w których konsonanse (oczywiście z wyjątkiem oktawy) i dysonanse są nieco rozstrojone w porównaniu z "antycznymi", ale pod względem czystości stroju żadna z możliwych do wygrania gam nie różni się od innych24.
Kiedy czytam to, co właśnie napisałem, nie dziwię się starożytnym, wznoszę oczy ku górze szukając absolutnej harmonii przynajmniej w niebiesiech, w materii z nie tego świata. A przy tym złorzeczę niewdzięcznej doczesności, która nie docenia ani piękna, ani magii związków liczbowych.
Wiarołomne odbicia idei w zwierciadle rzeczywistości.
Dopóki, jak znudzony szlachciura, tkwię w moim zaścianku, nosa zeń nie wychylając, dopóki jedyną drogą, jaką się poruszam jest raz na zawdy przez dziadów wytyczony gościniec; dopóki jedynymi punktami mego zainteresowania są ino początek i koniec podróży (oby bezpiecznej - bez rabusiów!), dopóty kwestia mierzalności świata wyrażona słowami liczbo-podobnymi nabiera wulgarnej wręcz czasoprzestrzennej prostoty, zawartej w przykładowym określeniu: "Stolica? Trzy dni drogi stąd!" Jedna wielkość: czas pomieszany z odległością nie gra najmniejszej roli, bo jest stały i niezmienny. Podobnie jak przesieka do sąsiada, albo dukt na kaplicę - trasa przecież nie roślina, więc ani się nie kurczy, ani nie rośnie. No, a droga, jak droga - trochę się wije, wznosi na pagórkach, ale poza tym płaska jak stół. To i pewnie cały świat taki płaski.
Kiedy jednak jestem antycznym światowcem żywo wojażującym między Italią a Egiptem (a niechby nawet "tylko" wzdłuż Nilu), i kiedy nocą podnoszę oczy, to któregoś wieczora dostrzegam wyraźnie różnicę w obrazie nieba nie wynikającą z dopustu pór roku. Tak jakbym kątem widzenia oczu omiatał inną część sfery upstrzonej zwierzyńcem gwiazd.
Geometrycznie rzecz biorąc, dla antycznego wędrowcy—myśliciela (przemierzającego kraje środziemnomorza z północy na południe) widoczność coraz to innego fragmentu sfery niebieskiej była dopuszczalna - już choćby i pod tym warunkiem, że Ziemia byłaby np. kulą zanurzoną we wnętrzu sfery nieba25.
Potrzeba matką matematyki.
Ale żeby wygodnie i pewnie podróżować - nie po omacku, abym mógł określić, gdzie jestem, potrzeba mi tego, co dzisiaj nazywam mapą. Ironią losu można by nazwać fakt, że pierwszą, do której mógłbym się odwołać, przemierzając morza i kontynenty otoczone białą plamą ziem nieznanych, była "mapa nie z tego świata" - mianowicie mapka nieba. Nic w tym dziwnego - brutalna oczywistość sprawia, że łatwiej odwzorować ten obraz, który widać okiem, niż ten z pamięci. Powierzchni Ziemi nie dane było nam było oglądać mimo ofiarności Ikara, natomiast niebo - widać co noc. Tak też pierwsza pojawiła się "mapa" nieba, na której gwieździste mrowie oswojono, nadając nazwy co większym skupiskom.
W ilu cięciach cyrkla zawiera się kosmos?
Chyba nic tak nie przeraża jak to, czego obecności doznajemy, a nie możemy namacalnie dostrzec26" ("Wieczerza popielcowa").
Wpadka z pitagorejskim trójkątem równoramiennym, dysonans poznawczy wywołany zobaczeniem "liczby nieistniejącej", usprawiedliwiał poniekąd zapał mędrców antycznych, z jakim oddawali się zadaniom "czysto" geometrycznym, starając się nie wplątać w dywagacje rachunkowe. Rozwiązania tzw. "zadań konstrukcyjnych" dopuszczały użycie tylko cyrkla i liniału, na których nie ma żadnej podziałki! Wydawać się to może dziwacznym utrudnieniem, ale daje badaczowi poczucie bezpieczeństwa, bo przez cały czas operujemy na tym, co "widać, słychać i czuć", czymś co jednocześnie widzi mędrca i szkiełko, i oko: odcinek, który wykreślam istnieje niezależnie od tego, czy umiem zapisać jego współmierność czy niewspółmierność z innym odcinkiem27.
Niemniej pamiętać należy, że tam, gdzie nie odmierzam wzorcem-podziałką, tam brak zera - miejsca od którego rozpoczynam pomiar; trudno zatem trafić na pojęcie początku, układu odniesienia.
Matematyka układu odniesienia.
Mnogość znanych rozwiązań antycznych zadań konstrukcyjnych, na których ani widu ani słychu o jakimkolwiek "układzie odniesienia" (a tym bardziej o jego początku), zdaje się istnieniu tej idei zaprzeczać28.
Niewątpliwym prekursorem układu odniesienia jawi się Eratostenes z Cyreny. On to, wpierw upewniwszy się, że nasza planeta jest kulą29, wymyślił pierwociny matematyki układu odniesienia: wykreślił siatkę geograficzną południków i równoleżników. Zaznaczając na niej położenie znanych współcześnie miast - w oczku, lub na boku siatki - stworzył pierwszą mapę (a nie tylko nowy obrazek!)30 świata. Nie była to co prawda analityczna dokładność, aleć zapotrzebowania na większą dokładność antyk nie zgłaszał.
W ten sposób stworzył on podwaliny dla opracowania co najmniej dwu wariantów struktury, jakiej dziś używamy pod nazwą układu współrzędnych. Pierwszy wariant dojdzie do skutku, kiedy pomysł siatki Eratostenesa zaadaptujemy do płaszczyzny, otrzymując kratownicę kartezjańskiego układu współrzędnych. Wariant drugi - biegunowy układ współrzędnych na sferze pojawi się, kiedy położenie poszczególnego oczka sieci podawać w odniesieniu do wyróżnionego równoleżnika i do wyróżnionego południka31.
W tym miejscu należy się parę słów o geometrii przestrzeni, w której możliwe jest zawieszenie sfery nieba, weń zaś - kuli ziemskiej. Z zadaniem tym bardzo wcześnie uporał się Euklides z Aleksandrii32, którego "Stoicheia"} ("Elementy geometrii") obowiązując przeszło 2000 lat miały ok. 1700 wydań33.
Nie wdając się w szczegóły: geometria tej przestrzeni wymaga, aby suma kątów każdego trójkąta równobocznego będącego ścianą czworościanu była stała i wynosiła 180 stopni Niezależność tego ("zastępczego") aksjomatu tak od czasu, (miejsca w) przestrzeni, układu odniesienia (zwłaszcza poruszającego się) - matematycznie oczywista, została jako pewnik przeniesiona na grunt zastosowań fizycznych i niezachwianie obowiązywała bodaj do czasów transformacji Lorentza34.
Zanim jednak zostały one uznane, koncepcja absolutnej geometrii długo ciążyła i przeszkadzała w pracy fizykom poszukującym jakiegoś wypełniacza kosmosu w obszarach, gdzie nas, ludzi, nie ma. Wypełniaczem tym miał być eter stanowiący jednocześnie doskonały, bo nieruchomy, układ odniesienia. Istnienie takiego fizycznego odpowiednika euklidesowej przestrzeni obalono dopiero pod koniec XIX wieku35.
Czas - wschodu i zachodu słońca.
Ponieważ nie jestem wielkim rzeczy znawcą, mogę się mylić, ale mam nieodparte wrażenie, że rzeczywistość antyku, rzeczywistość tak idealistów jak i empiryków, żyła trochę jakby poza czasem, że potrzeba matematyki czasu, czy potrzeba organicznego połączenia przestrzeni z czasem, czy w końcu - jakiegoś granicznego punktu czasu, nie była uświadomiona.
Przytoczony już wcześniej Eratostenes byłby zapewne niezmiernie rad, gdyby dowiedział się, że, kierując się jego naukami, Kolumb nie zawahał się odkryć Ameryki, a statki innego podróżnika - Magellana, płynąc wciąż na zachód, opłynęły w końcu kulę ziemską i zawinęły do rodzimego portu. Że nie dla wszystkich była to podróż szczęśliwa? Trudno, nauka wymaga poświęceń. Że załoga straciła na tej podróży kilka lat życia? Taki fach! Niezrozumiałe, niepojęte i przerażające było jednak dopiero to, że mimo przykładnego i sumiennego prowadzenia dziennika pokładowego, wszyscy byli na tej podróży tak naprawdę o jeden dzień do tyłu - wrócili we czwartek, podczas kiedy w Hiszpanii trwał już piątek36.
A co by to dopiero było, gdyby np. Sebastian del Cano, jeden z uczestników pierwszej wyprawy Magellana, miał brata bliźniaka? Mielibyśmy pierwszy odnotowany w historii paradoks bliźniąt wskutek poruszania się jednego z braci względem drugiego! Oczywiście żartuję.
Niemniej, ponieważ, jak powiadają, jest to „fakt autentyczny”, widać że nie potrzeba warunków ekstremalnych w skali mikro czy makro, aby wpadać w pułapki czasu, kiedy ignorować go w obliczeniach...
Matematyka ciała stałego zadaje kolejny tryumf materii nad ideą.
Doskonałość defektu.
Pojęcie ideału bardzo skomplikowała współczesna fizyka. Tak na przykład głęboko zakorzenionemu poczuciu doskonałości odpowiadają kryształy. Z wyglądu są nierzadko jak wielościany pitagorejskie. Przyciągają oczy regularnymi kształtami, ale także okazują niezwykłe właściwości: twardość (wiertną i tnącą), wytrzymałość na ściskanie. Do licznych walorów należy zaliczyć także ich "zachowania" optyczne.
Kryształ zda się kwintesencją porządku: tworzą go atomy (najczęściej w cząsteczkach) ułożone wobec siebie wedle danego wzorca wielościanów. Starożytni z pewnością fakt ten powitaliby z radością mówiąc: " oto przedmiot rzeczywisty, co doskonałość matematyczną ucieleśnia". Bo im dokładniej dany wzorzec odtworzony będzie w całej objętości kryształu, tym w naszym mniemaniu kryształ bliższy jest ideału. W naszym mniemaniu znaczy - w mniemaniu naszego oka. Geometria doznań wzrokowych jest bezwzględna...
A rzeczywistość? Trudno powiedzieć, czy istnieje chemicznie coś takiego, jak idealny kryształ: umiemy je hodować z pomijalnie małą liczbą zanieczyszczeń i defektów. Lecz ułomność niepokalanego poczęcia kryształu jest boleśnie rozczarowująca: tak wytworzony okazuje się być efemerydą, tworem bardzo nieużytecznym. Zazwyczaj pęknie pod byle pretekstem. Przyczyna zaś tkwi w tym, że jeśli w jakimkolwiek miejscu "pierwszym ciosem" rozdzielimy płaszczyzny atomów, zniszczenie pobiegnie przez kryształ jakbyśmy pruli szew sporządzony jedną nitką. Natomiast w naturalnych kryształach, tych o wielkiej wytrzymałości, znajdują się defekty pełniące podobną rolę jak zszywka, jak zbrojenie stalowe, które zatrzymuje rozpad płyty wskutek pęknięcia betonu. Tak więc, aby kryształ doskonałym był realnie, nie tylko "na oko", musi zawierać ziarno nieporządku, do idealnego wzorca musimy dosypać "piachu i śmieci". Czynimy to zresztą, produkując półprzewodniki. Bo kryształy prawie niepokalane, bynajmniej nie idealnie czyste, ale tak dobrze oczyszczone, jak potrafi to zrobić współczesna technika, to poroniony pomysł idealistów - twory czyste w życiu do niczego się nie nadają.
Podsumowanie.
Nigdy, przenigdy nie chciałbym być podejrzewany o wrogość wobec matematyki. Lektura niejednego zagadnienia była jak wicher, który czapkę z głowy zdmuchnął. Ale podziwiając genialność tego czy innego podejścia, struktury, przepisu, podziwiam raczej potęgę ludzi, którzy matematykę wymyślali wedle potrzeby, lub zamiłowania do rozrywek37. To szarawa codzienność, w jakiej wyrastamy, może sprawiać, że uważamy fizykę za "czystą" teorię, a to z kolei każe zepchnąć ją na manowce matematycznego abstraktu. Istotą fizyki natomiast jest pomiar. Z pomiaru w toku kolejnych przybliżeń, dokładnie nazwanych uproszczeń, rachunku błędów38 (to zastosowanie rachunku błędów pozwoliło Milikanowi udowodnić istnienie elementarnego ładunku elektrycznego) pomiarowych uzyskujemy asymptotę wyniku w układzie współrzędnych mierzonych parametrów; z tych danych "odgadujemy" równość, wzór. To fizycy, szukając krótkich, zwartych, przejrzystych i eleganckich wyrażeń (które dla danego zjawiska pozwalają wyliczyć wyniki bliskie wynikom pomiarowym), tworzą modele matematyczne, wedle których świat jest raz superstruną, raz płaszczakiem, a czasem "gonokokiem". Matematyka jest jak pieniądz: w danym czasie i miejscu używa się odmiennej waluty, a lepsza wypiera gorszą39.
© Adam Cebula, Ryszard Krauze, Wrocław, 30 maja - 12 czerwca 2001. Koniec Przypisy1 w przeciwieństwie do inwokacji W. Rybczyńskiego (np. - "Problemy", nr 8, 1949 r), ta wolna jest od błędu... 2 cytuję z pamięci 3 "Książę i żebrak" 4 będący na oko tym, co widzimy między dwiema kreskami na belce z irydu i platyny w skansenie od Paryżem (stara definicja; nowa jest dla laika bardzo nieprzyjemna) 5 {n=1,2,3...} 6 można oczywiście zmienić wzorzec, jednostkę długości—odległości tak, aby wszystkie pomiary w sytuacjach "zdrowo--rozsądkowych" dawały wielokrotność tej nowej jednostki, ale trzeba by wprowadzać nową jednostkę za każdym razem, kiedy wynik różni się od krotności wzorca o "troszeczkę" - nie taki jest wszak sens wzorca! 7 liczbą następną staje się bieżąca powiększona o jedynkę 8 których ideę głosił Demokryt przejąwszy ją od Strabona. 9 śladem przywiązania budowniczych piramidy Cheopsa do wymienionych tekście liczb jest komnata królewska o następujących proporcjach: (długość przekątnej najmniejszej ściany) do (długości krawędzi najdłuższej) do (długości przekątnej wielościanu) mają się do siebie jak 3 do 4 do 5; stąd egipskość takiego trójkąta 10 starożytnym (przypisuje się to Pitagorasowi) wystarczyły rozważania o parzystości i nieparzystości a, b; nie-naturalność 11 jest nie mniej pospolitym od pojedynczej piszczałki, ale strunę łatwiej wykonać 12 pudło (rezonansowe) możemy "wynaleźć" później... 13 w istocie liczbę akordów można by policzyć z rachunku prawdopodobieństwa... 14 starożytni nie chcieliby tego wiedzieć - to nie żadna magia, a czysta fizjologia organu Cortiego w uchu: prawie zawsze, kiedy odczuwamy konsonans zachodzi zgodność harmonicznych; tony te towarzyszą co prawda rzeczywistym tonom podstawowym, ale "powstają" w błonie bębenkowej również wskutek brzmienia tonu podstawowego. Badany stwierdza tym większe odczucie konsonansu, im lepiej pokrywają się harmoniczne podawanych tonów. 15 na początek najlepiej uznać słowo "oktawa" po prostu za nazwę historyczną i nie dziwić się temu, że 2:1 ma jakiś związek z 8... 16 dur: sekunda, wielka tercja, kwarta, kwinta, wielka seksta, wielka septyma, oktawa; moll: sekunda, mała tercja, kwarta, kwinta, mała seksta, mała septyma, oktawa 17 zapis wielką czcionką {C-dur} zamiast {c--dur} podkreśla "durowość", "większość" tonacji 18 patrz np.: A. Drzewiński, J. Wojtkiewicz "Opowieści z historii fizyki" 19 "Metafizyka", A.5. 985 b. 23; cyt. za W. Witwicki: "Fedon" Platona. 20 takie absolutne, czyste strojenie uzyskać można w zasadzie jedynie w przypadku instrumentów smyczkowych (bo tylko w nich na stałe strojone są wyłącznie struny puste), lecz nie w instrumentach o ustalonej wysokości każdego tonu w danej tonacji 21 ponieważ 22 Stiefel, 1541; Werckmeister, 1700 23 opartej od 1939 r. na tonie1a = 440 Hz 24 oznaczmy przez a interwał pomiędzy poszczególnymi dźwiękami stroju; po 12 odstępach (dźwiękach) a$ dochodzimy do oktawy, czyli a12 = 2, zatem a = 25 pogodzenie się zaś z kulistością Ziemi nie byłoby kłopotliwe - kulę od dawna uważano za najdoskonalszą z brył, więc idei, że stąpamy po najdoskonalszej, należało tylko przyklasnąć! 26 łagodniej wyraził to Giordano Bruno: Nie mogę też pokochać rzeczy, której bym nie zobaczył. 27 Pitagoras przyjmował, że dwa odcinki AC i BD są współmierne, o ile istnieje wspólna miara (wzorzec), która w odcinku AC odkłada się a razy, natomiast w odcinku BD odkłada się b razy; rzecz jasna tak a, jak b są liczbami całkowitymi. 28 niemniej z lektury dzieł dawnych przytoczyć należy przekonanie Pitagorasa, że Ziemia jest centrum wszechświata; pytanie tylko, czy postrzegał owo miejsce jako środek wibrujących harmonijnie sfer niebieskich, czy jako punkt, w którym zaczepiamy dociekliwe ostrze cyrkla badań geometrii kosmosu (badań geometrycznych rzecz jasna - rozwiązywanie zostało wszak całkowicie zwizualizowane) 29 jako pierwszy wiarygodnie zmierzył promień Ziemi, dowodząc jej kulistego kształtu 30 III w. p.n.e.! 31 oczywiście pomysł dopracować mogli tylko ci, którzy nie lękali się liczb niecałkowitych i znali liczbę zero. 32 żyjący ok. 365-300 p.n.e. 33 cyt. za: J. Wolski, Historia powszechna, wyd. 1965, s.222. 34 Hendrik A. Lorentz oraz Henri Poincare w latach 1900-1904 stworzyli podwaliny matematyki rzeczywistych układów odniesienia, w których zachowane są prawa fizyki stwierdzone doświadczalnie. Dane miejsce rzeczywistości nie jest opisane absolutnym i niezmiennym wektorem położenia, któremu towarzyszy dodatkowy parametr - absolutny czas, lecz stanowi czterowektor w przestrzeni Minkowskiego; takie ujęcie dopuszcza zapis czasu jako liczby zespolonej o rzucie niezerowym tylko na osi urojonej, tj. której wersorem jest 35 Albert A. Michelson, w latach 1881-1887. 36 fakt istnienia linii zmiany daty nie był wówczas znany 37 Pascal, Fermat... 38 rachunku niedokładności zwanych fachowo niepewnościami 39 waluta, nie pieniądz bity z kruszcu; prawo Kopernika wciąż obowiązuje. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
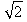 nie była konieczna
nie była konieczna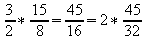
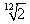 = 1,059, tak więc a2 = 1,121 wobec 1,125 większego całego tonu, oraz 1,111 mniejszego całego tonu.
= 1,059, tak więc a2 = 1,121 wobec 1,125 większego całego tonu, oraz 1,111 mniejszego całego tonu.